THE NOMOTHETIC THEOREMor dealing with abstract, general, or universal statements or laws The Nomothetic Theorem acknowledges that our universe exists in the context of a balance between opposing forces constantly struggling against each other. It is therefore fitting that the theorem itself is a dualism. It consists of two theories that are themselves interdependent as polar opposites. The Nomothetic Theorem says, "Continuous random motion exists in every complex system, and every complex system, when not influenced by any outside force, will move toward increasing levels of stability." Thus, we have The Theory of Volatility and The Theory of Stability. The Nomothetic Theorem explains complex dynamic systems. It explains how life can survive in what might otherwise be a random and chaotic environment. It explains the characteristics of complex systems, the arrow of time, and the regulated move toward maximum entropy. It provides an explanation for the sequential unfolding of events that goes beyond simple cause-and-effect, and it provides a new predictive tool. Background Complexity swirls around us and touches almost every aspect of our life. Our world includes mechanical systems, energy systems, chemical systems, biological systems, social systems, information systems, economic systems, and many more. These systems overlap, interweave, and collide to create a cacophony of confusion in our daily environment. Yet somehow, we manage to deal with this vast complexity. In fact, the survival of life in a complex, hostile, ever-changing environment seems like a miracle. How can something as fragile as life exist amid changing temperatures, pressures, heat, light, and an amazing array of chemicals? Charles Darwin answered this question by proposing the concept of natural selection and the theory of evolution. While this helps explain how organisms adapt to changes in their environment over long periods of time, it does not address the question of how we survive daily interaction with complexity. Higher order life forms depend on finding resources (food and water) and a protective environment (shelter). If the universe were entirely random and chaotic, this would not be possible. The fact that life forms can find the necessities for their sustenance says a great deal about complex systems: There is some order in the universe! There is some consistency. There are recognizable patterns. Pattern recognition is at the heart of prediction, and prediction is at the heart of man's ascendency to dominance on this planet. People learn at an early age that prior events are the cause of future events. This belief in cause-and-effect is so pervasive that the legal systems in the western world are based on the concept of individual responsibility. People should be held responsible for their actions because those actions result in future outcomes that affect others. Most people live and think in a linear world. When linkage is discovered in a chain of events, recognition of a causal input allows the prediction of the resulting outcome. Cause-and-effect is relevant when analyzing direct relationships between individual entities, but it fails as a predictive tool when trying to forecast outcomes in dynamic complex systems. Complexity encompasses such things as simultaneity, covariance, second and third derivative motion, and different outcomes from the same inputs. A better model is required for our incredibly complex world. THE THEORY OF STABILITY "Every complex system, when not influenced by any outside force, will move toward increasing levels of stability." The Theory of Stability rests on the axiom that: "Energy seeks to cure an imbalance." This simply means the movement of energy is that property in the universe which causes an imbalance to persistently move toward balance. Energy is directional. Energy can perform work because it wants to move. Starlight wants to radiate outward. Heat wants to radiate outward. Liquid under mechanical pressure wants to spray outward. This desire for energy to cure an imbalance subsumes Aristotle's statement that "Nature abhors a vacuum." By curing imbalance, energy seeks to increase system stability. The only other way higher levels of stability can be achieved is if work is performed by a non-conservative force that transfers energy out of the system. Energy dissipation leads to increasing levels of stability. To understand the Theory of Stability, we must first make sure we agree on the definition of the word stability. For the purpose of this theory, stable does not mean static and unchanging. Unchanging may, in some cases, be the ultimate level of stability, but systems seek various levels of intermediate stability by coming into balance on their journey toward maximum entropy. Stable means operating over time, or existing at any moment in time, within a limited range of change, or in a known or familiar manner. Thus, a pendulum swinging back and forth is stable. A planet continuously orbiting the sun is stable. A pendulum on a clock sitting on a planet spinning on its axis and orbiting the sun is stable, at least temporarily. When the clock winds down and the pendulum stops swinging, it will enter a new level of stability. An important element of stability is predictability. But predictable does not mean simply repetitious. Predictable means operating within a limited range or in a deterministic manner that allows us to forecast the next location, the next formation, or next event. Thus, stability means order and dependability over time. Stability implies a "balance" of the forces acting on a system. An airplane flying at 550 mph across the country is not static, but it can be stable. When aerodynamic lift is in balance with the force of gravity, and engine thrust is in balance with drag, the airplane can be thought of as stable. From this example, we can perhaps understand that stability does not mean unchanging. The airplane is very dynamic. But we can predict where it will be. And we can depend on our prediction. A stable system can therefore include change. In fact, constant change is itself a form of stability. One way to classify stability is to measure the surprise factor or the deviation from the expected next point position or value. A highly stable system allows for a high degree of confidence in the next point prediction. The next concept to understand is "drift." As stated above, stability does not mean unchanging. The net change to the system over time is called "drift." Drift can be thought of as the average result of the net imbalance of all forces on a system causing the system to trend over time. We tend to think in a linear fashion. But just as complex systems can be multi-dimensional, drift can also be multi-dimensional. However, most practical applications don't have to be complex to be useful. Continuing with our example of an airplane, if all the forces are in balance on a helicopter, it will hover in exactly one position. If a fixed-wing plane is stable, thrust must exceed drag so air can move over the wings. This is necessary for it to remain flying. Therefore, the plane must travel through the air. This travel is called system drift. The drift may be west to east across the country. If there is a wind from the north, the drift may be pushed southeast across country. If the plane is planning to land, the drift may be southeast and descending. As we shall see later in the Theory of Volatility, stable systems are subject to volatility (such as clear air turbulence) and to "events" (such as an engine failure). Volatility does not cause a lasting change to drift. But "events" do influence drift. THE THEORY OF VOLATILITY "All complex systems experience continuous random change." Since motion is a common subset of change, motion is frequently substituted for the word change. The Theory of Volatility depends on a belief in sequential motion (or change) by discrete elements such that: "No one thing can be in two different places (or in two different states) at the same time." And further, in the space-time continuum of four dimensions: "Every unique point in all four dimensions can only be occupied by one unique thing (in one state) at the same instant in the same time frame." One thing cannot be in two places at the same time, nor can two things occupy the same place at the same time. Any violation of this axiom should make us suspect that what appears as one thing is in fact two things. Or what appears to be two different places is in fact the same place. Or what appears to be the same time is in fact two different times. For our purposes, the most interesting aspect of this axiom is the relationship between different locations and time. In all dimensions, the concept that defines the space or distance between two locations is dependent on sequential motion; and sequential motion is dependent on time. In a broader sense, three-dimensional space cannot exist without time, and time is meaningless without motion (or change) to define space. Motion is omnipresent. Change is all around us. Continuous change facilitates system movement toward ever-increasing levels of stability. The existence of continuous random motion may seem extremely simplistic, but it has many important implications, particularly when combined with the Theory of Stability. Decay is a prime example. Decay comes from random motion at a very low level in a system of molecules or atoms. The continuous random volatility found in complex systems presents itself as fluctuations around a central point of stability. Since the forces that cause closed systems to evolve toward stability counteract volatility, the Theory of Volatility, while stating that there are random fluctuations, accepts the fact there is a limit to the degree of normal fluctuation in a closed system. The outer limits of the normal, random fluctuations define a normal range of volatility. By definition, motion or changes that occur within the normal range of volatility are random. Therefore, the Theory of Volatility says, "The next movement from any point within the normal range of volatility is unpredictable." The normal range of volatility contains one or more ultimate points of stability. Although the size of the range of volatility may itself change over time, at any moment in time, there is a discrete and measurable range of volatility known as the "normal range of volatility."
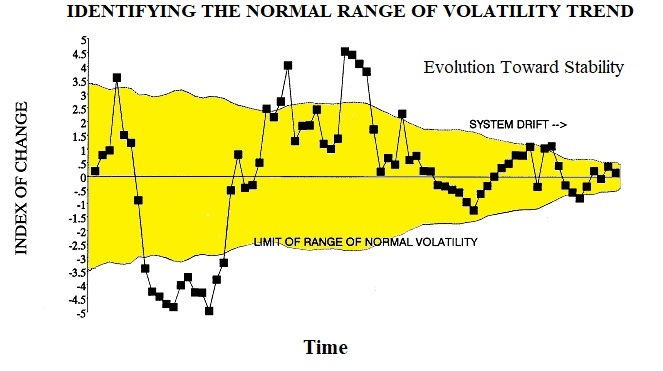
The "norm" is the point of stability that the system is evolving toward and is found within the normal range of volatility. Frequently, but not necessarily, the norm is close to the mid-point of the normal range of volatility and represents a point where forces are in balance within the system. It is possible for there to be more than one point of ultimate stability. In addition to discreet points, stability may be defined by an orbit or a range of oscillations. However, in all cases, there will be an accompanying range of volatility. Due to system drift, the point of stability that defines the norm (and its surrounding range of volatility) is, in fact, a trend that is continually evolving over time toward stability (equilibrium or higher entropy) in direction, degree, and dimension.
Random motion takes on special significance when it becomes a deviation from the norm that exceeds the normal range of volatility. An extreme movement beyond the normal range of volatility is called an "event." The event isn't the deviation. The event is what causes the deviation. An event may be triggered by something internal to the system or it may be from the introduction of external energy, for example, when two systems (or subsystems) intersect. The effect of an event is to put pressure on the norm and perhaps ultimately move the norm unless there is an equal and opposite "balancing" event. An event, or a series of events, may change the rate of change of a trending norm or start a new trend. The influence on the norm is a factor of time and degree of deviation. In some applications, the usefulness of the Nomothetic Theorem comes from its prediction of the next event or next-point position. This is a very brief introduction to The Nomothetic Theorem. |
 |
| Developed by John Boyle. Published by Tryqit LLC. Learn more here. |
| A Real World Application Of The Nomothetic Theorem |